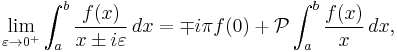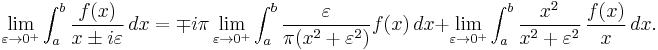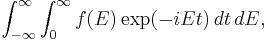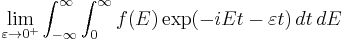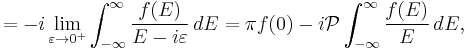Sokhatsky–Weierstrass theorem

The Sokhatsky–Weierstrass theorem (also spelled Sokhotsky–Weierstrass theorem, and also called the Sokhotski–Plemelj formula,^[1] or the Weierstrass theorem, not to be confused with various other theorems called the "Weierstrass theorem") is a theorem in complex analysis, which helps in evaluating certain Cauchy-type integrals, among many other applications. It is often used in physics, although rarely referred to by name. The theorem is named after Yulian Sokhotski, Karl Weierstrass and Josip Plemelj.

1 Statement of the theorem
2 Proof of the theorem
3 Physics application
4 References
- 4.1 References that refer to the theorem by name

Statement of the theorem

Let ƒ be a complex-valued function which is defined and continuous on the real line, and let a and b be real constants with a < 0 < b. Then

$\lim_{\varepsilon\rightarrow 0^%2B} \int_a^b \frac{f(x)}{x\pm i \varepsilon}\,dx = \mp i \pi f(0) %2B \mathcal{P}\int_a^b \frac{f(x)}{x}\, dx,$

where $\mathcal{P}$ denotes the Cauchy principal value.

Proof of the theorem

A simple proof is as follows.

$\lim_{\varepsilon\rightarrow 0^%2B} \int_a^b \frac{f(x)}{x\pm i \varepsilon}\,dx = \mp i \pi \lim_{\varepsilon\rightarrow 0^%2B} \int_a^b \frac{\varepsilon}{\pi(x^2%2B\varepsilon^2)}f(x)\,dx %2B \lim_{\varepsilon\rightarrow 0^%2B} \int_a^b \frac{x^2}{x^2%2B\varepsilon^2} \, \frac{f(x)}{x}\, dx.$

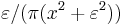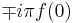For the first term, we note that $\varepsilon/(\pi(x^2%2B\varepsilon^2))$ is a nascent delta function, and therefore approaches a Dirac delta function in the limit. Therefore, the first term equals $\mp i \pi f(0)$ .

For the second term, we note that the factor 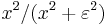$x^2/(x^2%2B\varepsilon^2)$ approaches 1 for |x| >> ε, approaches 0 for |x| << ε, and is exactly symmetric about 0. Therefore, in the limit, it turns the integral into a Cauchy principal value integral.

Physics application

In quantum mechanics and quantum field theory, one often has to evaluate integrals of the form

$\int_{-\infty}^\infty \int_0^\infty f(E)\exp(-iEt)\,dt\, dE,$

where E is some energy and t is time. This expression, as written, is undefined (since the time integral does not converge), so it is typically modified by adding a negative real coefficient to t in the exponential, and then taking that to zero, i.e.:

$\lim_{\varepsilon\rightarrow 0^%2B} \int_{-\infty}^\infty \int_0^\infty f(E)\exp(-iEt-\varepsilon t)\,dt\, dE$

$= -i \lim_{\varepsilon\rightarrow 0^%2B} \int_{-\infty}^\infty \frac{f(E)}{E-i\varepsilon}\,dE = \pi f(0)-i \mathcal{P}\int_{-\infty}^{\infty}\frac{f(E)}{E}\,dE,$

where the latter step uses this theorem.

References

^ Blanchard, Philippe; Brüning, Erwin (2003). Mathematical Methods in Physics. Boston: Birkhauser. ISBN 0817642285. Example 3.3.1 4.

Weinberg, Steven (1995). The Quantum Theory of Fields, Volume 1: Foundations. Cambridge Univ. Press. ISBN 0-521-55001-7. Chapter 3.1.
Merzbacher, Eugen (1998). Quantum Mechanics. Wiley, John & Sons, Inc. ISBN 0-471-88702-1. Appendix A, equation (A.19).

References that refer to the theorem by name

Most sources that use this theorem, as mentioned above, refer to it generically as "a well-known theorem" or some variant. Here are some sources that refer to the theorem by name: